So Bankroll if $10k:
NBA Total for this game is, UNDER 200 +100,
OVER 200 1/2 +110.
Odds to tie at 200 for this game is 2% ( which represent losing one side out right.)
How much should I wager?
Both side has +EV.
Thanks in advance.
NBA Total for this game is, UNDER 200 +100,
OVER 200 1/2 +110.
Odds to tie at 200 for this game is 2% ( which represent losing one side out right.)
How much should I wager?
Both side has +EV.
Thanks in advance.

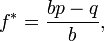 where:
where:

 Maybe I'll calculate a fair line tomorrow and see what the true percentages should be and try part 1 again. It will still be profitable, though.
Maybe I'll calculate a fair line tomorrow and see what the true percentages should be and try part 1 again. It will still be profitable, though.