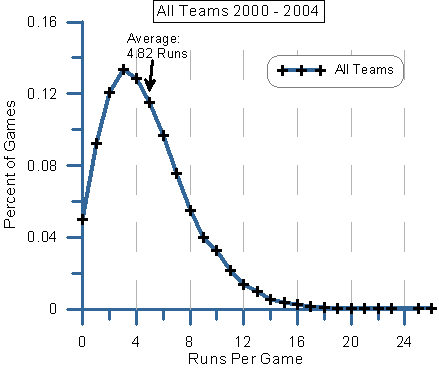
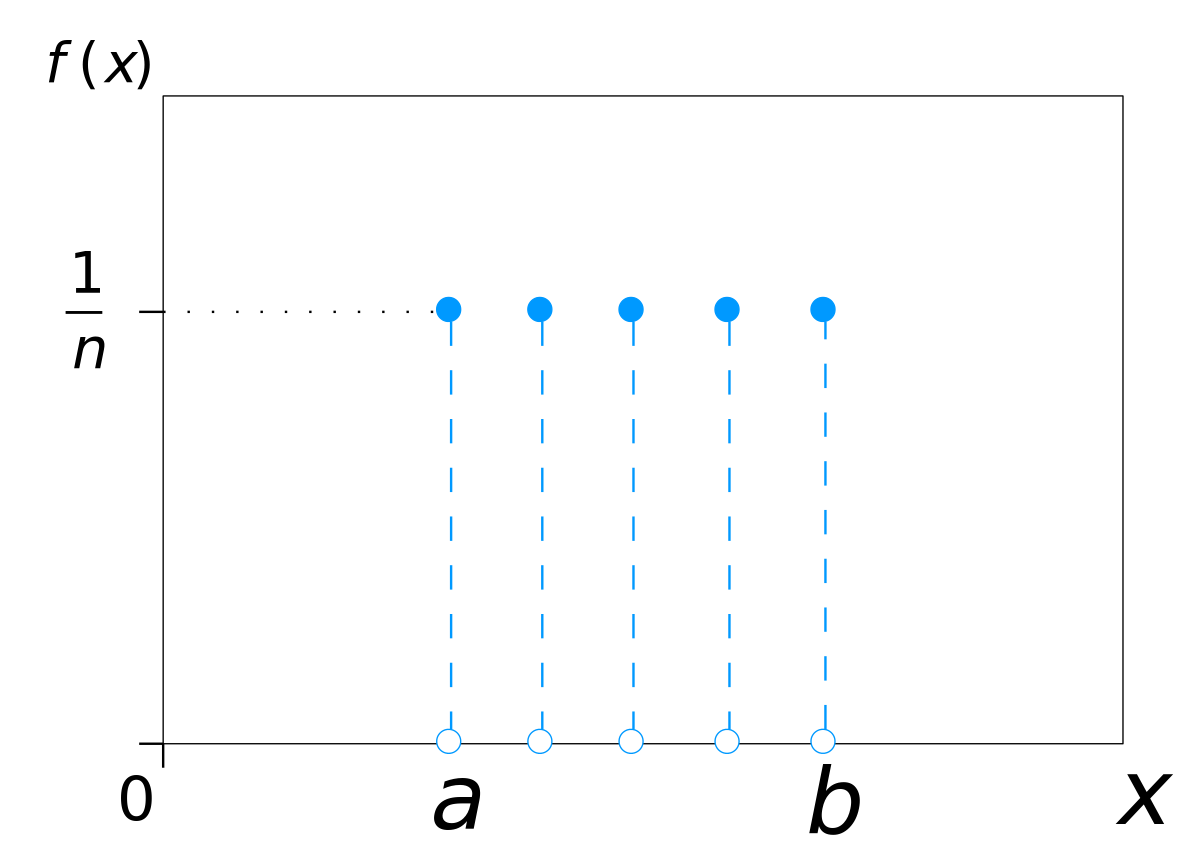
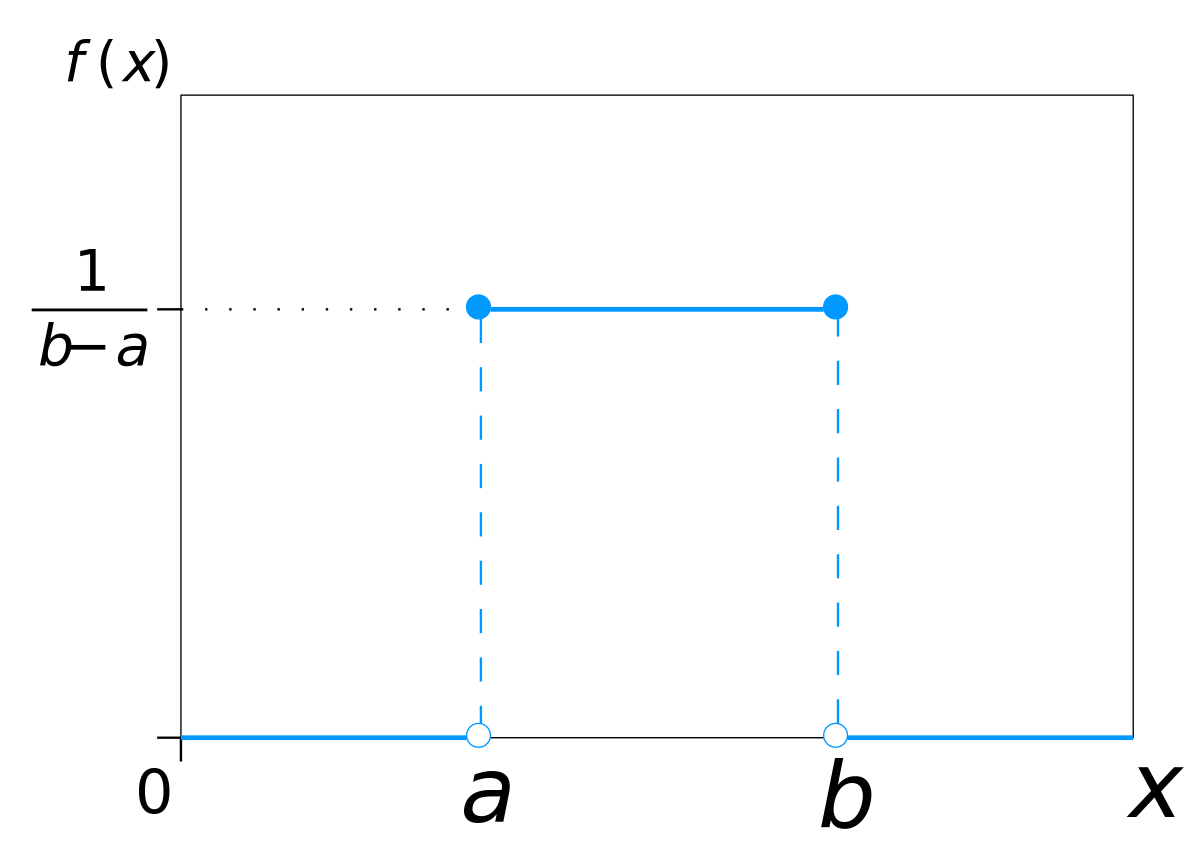
I like to think of myself as an experienced sports modeler that is well versed in all manner of regression and classification techniques, however I've drawn somewhat limited inspiration as to how to model standard deviation.
The 'true' standard deviation of underlying game is not even known at the end of the game, as compared to usual regression and/or classification targets such as the margin of victory or who covered ATS.
The only way I can think of to model standard deviation is through Monte Carlo simulation. Bayesian techniques may also work, but there still has to be some manner of characterizing the distribution of a mean for the likelihood function.
Has anyone thought about this themselves?
The 'true' standard deviation of underlying game is not even known at the end of the game, as compared to usual regression and/or classification targets such as the margin of victory or who covered ATS.
The only way I can think of to model standard deviation is through Monte Carlo simulation. Bayesian techniques may also work, but there still has to be some manner of characterizing the distribution of a mean for the likelihood function.
Has anyone thought about this themselves?