Using the binomial distribution to determine the probability of runs scored.

[Gradius]

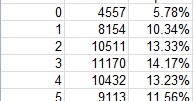
I was watching some videos about the binomial distribution on Khan Academy, and I thought maybe I could use this for baseball. Let's say I model a game between the Yankees and Red Sox (this is just an example), and I get an expected total of 8.52, I would then like to know what the probability of both teams combining to score 1 run, 2 runs, 3 runs, etc... (anything integer below 8.52), and then any integer above 8.52. In baseball, you can score as many runs as you can (since there is no time limit), but obviously, the odds of both teams combining for 30+ runs are extremely low (probably under 1%), and with an output of 8.52 total runs, the extremes (1 run scored and 30+ runs scored), are going to be a lot lower than 7, 8, or 9 runs scored. Is there a method or calculator I can use to determine this probability, if I have a have a model that outputs totals?

If what I am saying is hard to understand, please tell me. Thank you.

[oddsfellow]

This may help in your quest

http://walksaber.blogspot.co.uk/2012/06/on-run-distributions-pt1.html

[agendaman]

in the long run you will go broke i am a mathematician all these things have been tried before

[Gradius]

Oddsfellow: Thanks for that link. While it didn't quite directly answer my question, the process of trying to obtain a probability distribution was helpful. The link supplied used a league average runs per game distribution of 4.45 runs per game, and the league average today is about 4.2 runs per game, which would skew some of the results if I used their formula as a probability distribution. Again, the information was helpful, and I thank you for it.